Arranjo e combinação
Na matemática, a diferença fundamental entre arranjo e combinação é a ordem dos objetos. No arranjo a ordem dos objetos é muito importante, ou seja, os objetos devem obedecer uma ordem estipulada. Em contrapartida, no caso de uma combinação, a ordem não tem importância nenhuma.
| Arranjo | Combinação | |
|---|---|---|
| Ordem | É importante. | Não é importante. |
| Significado | Arranjo refere-se às diferentes maneiras de organizar um conjunto de objetos em uma ordem sequencial. | Combinação refere-se às várias maneiras de escolher itens entre um grande conjunto de objetos, de modo que sua ordem não importa. |
| Denota | Arranjo. | Seleção. |
| O que é | Elementos ordenados. | Conjuntos não ordenados. |
| Exemplo de questão |
Um número de telefone é formado por 9 algarismos, de 0 a 9. Sendo assim, quantos números de telefone diferentes nós podemos ter? |
Entre um grupo com 10 alunos, o professor deve escolher 3 para fazer uma apresentação. Determine de quantos modos diferentes o professor poderá escolher esses alunos. |
Definição de Arranjo
Na análise combinatória, arranjo são os modos diferentes de organizar os objetos de um conjunto, em uma ordem específica. Isto implica toda a disposição ou rearranjo que for possível.
Por exemplo, toda o arranjo possível criado com letras x, y, z seria:
- Usando todos os três de cada vez: xyz, xzy, yxz, yzx, zxy, zyx;
- Usando dois de cada vez são xy, xz, yx, yz, zx, zy.
Exemplo de arranjo na prática
Digamos que a senha do seu armário é 5432. Se você inserir 4325 nele, ele não será aberto porque é uma ordem diferente.
Os arranjos possíveis para 2, 3, 4, 5 são: 5432, 5423, 5324, 5342, 5234, 5243, 4532, 4523, 4325, 4352, 4253, 4235, 3542, 3524, 3425, 3452, 3254, 3245, 2543, 2534, 2435, 2453, 2354, 2345.
Podemos dizer que a senha do seu armário é um arranjo específico de 2, 3, 4 e 5. Se o seu armário funcionasse por combinação, você poderia inserir qualquer uma dos arranjos acima e ele abriria!
Fórmula para calcular arranjos simples
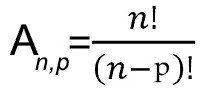
n = Quantidade total de elementos no conjunto
P = Quantidade de elementos por arranjo
Definição de Combinação
A combinação é definida como as diferentes formas de seleção de um grupo, tendo alguns ou todos os itens de um conjunto, sem que a ordem importe.
Como exemplo, essas seriam as combinações possíveis com as letras x, y, z:
- Quando todas as letras forem usadas, a única combinação será xyz.
- Quando duas de três letras forem utilizadas, as combinações possíveis são xy, xz, yz.
Fórmula para calcular combinação

Exemplo da diferença entre arranjo e combinação
Suponha que exista uma situação em que você tenha que descobrir o número total de amostras possíveis de dois dos três objetos A, B, C. Primeiramente você precisa entender se a questão está relacionada à arranjo ou combinação, e a única maneira de descobrir isso é verificar se a ordem é importante ou não.
Se a ordem é significativa, então a questão está relacionada à arranjo, e as possíveis amostras serão AB, BA, BC, CB, CA, CA. Nesse caso, AB é diferente de BA, BC é diferente de CB e AC é diferente de CA.
Se a ordem for irrelevante, a questão está relacionada à combinação, então as amostras possíveis serão AB, BC e CA.
Leia também sobre a diferença entre Algarismo, número e numeral.